声明:我已委托「维权骑士」(rightknights.com)为我的文章进行维权行动。
二叉树的遍历算法
二叉树遍历算法是面试过程中的常见考题,面试官常常要求应聘者写成树的三种遍历(前序、中序、后序)算法,当然要完成这个任务非常简单,每一种遍历方式的代码不超过10行。假设树中节点的结构如下
class TreeNode{
int val;
TreeNode left,right;
}
树的递归遍历算法
树的前序遍历
void preOrder(TreeNode root){
if(root==null) return ;
System.out.println(root.val);
preOrder(root.left);
preOrder(root.right);
}
树的中序遍历
void inOrder(TreeNode root){
if(root==null) return ;
inOrder(root.left);
System.out.println(root.val);
inOrder(root.right);
}
树的后序遍历
void postOrder(TreeNode root){
if(root==null) return;
postOrder(root.left);
postOrder(root.right);
System.out.println(root.val);
}
整体上,三者的基本结构是一样的,只是输出的位置发生了变化。
考虑到递归调用有的时候会出现Stack Overflow的问题,为此,我们还需要会写非递归调用的树的三种遍历。具体的实现形式可以基于Stack实现。
基于Stack 的实现方法
前序遍历
三种遍历算法中,树的前序遍历最为简单,因为他不存在状态回溯。
基本实现的思路如下:首先我们先将根节点压入到Stack中,然后进入一个循环:从Stack顶部取一个节点,输出这个节点,再将节点的左右非空子节点( 按照先右节点再左节点的顺序 )放入到Stack,直至Stack中为空,结束循环,遍历结束。 代码实现如下:
void preOrderWithStack(TreeNode root){
if(root==null) return ;
Stack<TreeNode> stack =new Stack();
stack.add(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
System.out.print(node.val);
if(node.right!=null){
stack.push(node.right);
}
if(node.left!=null){
stack.push(node.left);
}
}
}
中序遍历
一种简单的情况
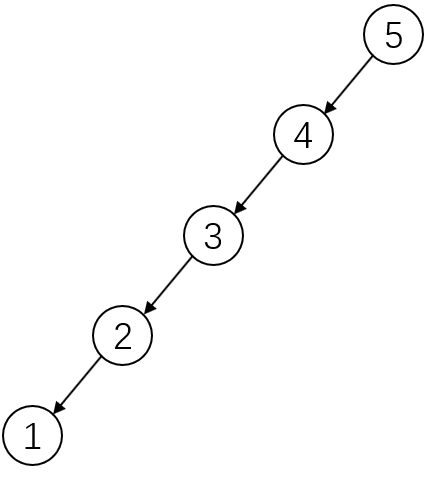
在编写中序遍历的代码之前,我们先来看看一种情况,也就是“丿”撇字型的数,所有的节点的右子树均为null。在这种情况下,我们可以先将这个撇要入到栈中,然后一边pop一边输出,得到结果就是我们想要的中序遍历。
具体代码比较简单,如下
void inOrderWithStack(TreeNode root){
if(root==null) return;
Stack<TreeNode> stack = new Stack();
TreeNode node = root;
while(node!=null){ // ①查找root树的最小元素
stack.push(node);
node = node.left;
}
while(!stack.isEmpty()){ // ②依次弹出栈中的元素
node = stack.pop();
System.out.print(node.val);
}
}
当然这个还离我们的想要的二叉树的中序遍历有一些距离。
从结构上,撇字形的树和二叉树的区别在于二叉树可能存在右子树,为此,当我们将一个节点输出后,我们还没有进行树的右子树的遍历,为此我们需要这个节点的右子树进行中序遍历,
也就是当我们输出一个节点node后,要需要对这个节点的右子树进行检查,如果它不为空,那么我们需要对它进行中序遍历,回到上面一段代码中的①处,不同的是此时的root变成了node。为此,我们可以代码进行调整得到我们需要的中序遍历。
最终的代码实现
具体代码如下
void inOrderWithStack(TreeNode root){
if(root==null) return ;
Stack<TreeNode> stack = new Stack();
TreeNode node = root;
while(!stack.isEmpty()||node!=null){
while(node!=null){ //①查找root树的最小元素
stack.push(node);
node = node.left;
}
node = stack.pop(); // ②弹出栈顶元素,并输出
System.out.print(node.val);
node =node.right; // ③node指向右子树
}
}
后序遍历
相比前面这个遍历方式,后序遍历的实现需要一定的技巧
比较简单的方法
对于一个树的后序遍历, 顺序如下:左子树 - 右子树 - 当前节点,我们可以看着 当前节点 - 右子树 - 左子树的逆序,这样我们就可以采用的类似前序遍历的方法,再将得到的中间结果进行逆序,输出即可,中间结果可以储存在Stack中或者ArrayList中,具体实现如下:
void postOrderWithStack(TreeNode root){
if(root==null) return ;
Stack<Integer> result = new Stack();
Stack<TreeNode> stack = new Stack();
stack.add(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
result.add(node.val);
if(node.left!=null){
stack.push(node.left);
}
if(node.right!=null){
stack.push(node.right);
}
}
while(!result.isEmpty()){
int val = result.pop();
System.out.print(val);
}
}
另一种实现方式
上面中方式巧妙借助了前序遍历解决了问题,现在我们采用另一种方式解决这个问题。
我们还是先考虑刚才的那一种特殊情况,对于撇字形 的树,他的后序遍历就比较简单了,具体如下
void postOrderWithStack(TreeNode root){
if(root==null) return;
Stack<TreeNode> stack = new Stack();
TreeNode = node ;
while(node!=null){
stack.push(node);
node=node.left;
}
while(!stack.isEmpty()){
node = stack.pop();
System.out.print(node.val);
}
}
和中序遍历类似,我们缺少对节点右子树的检查 。不同的是,中序遍历是先输出再检查右子树 ,这里我们需要先检查左子树,再输出节点 :当我们检查栈顶元素时,如果之前输出的节点是栈顶元素的左子树,这意味着当前节点的左子树输出完毕,需要进行右子树的后序遍历;如果当前输出节点是栈顶元素的右子树,则当前节点的右子树输出完毕,直接pop,输出当前节点。 具体代码实现如下:
void postOrder(TreeNode root){
if(root==null) return;
TreeNode node = root;
TreeNode pre = null;
Stack<TreeNode> stack = new Stack<>();
while(!stack.isEmpty()||node!=null){
while(node!=null){
stack.push(node);
node = node.left;
}
node = stack.peek();
if(node.right ==null ||node.right==pre){ // 右子树为空或者右子树已经输出
System.out.println(node.val);
node = stack.pop();
pre = node;
node =null; // 防止重新进入循环
} else {
node = node.right;
}
}
}